DimensionEngine
Never convert units again

Home  |   QuickStarts: 20 Sec  5 Min  |   Documentation   |  Solved Textbook Probs.

References

User's Guide



1. Introduction

DimensionEngine is a calculator that handles and performs calculations using dimensional units, automatically converting them correctly within equations, outputting answers in user-selected default or explicit units, and indicating when inconsistencies are present in your calculations so that errors can be identified and corrected.



The DimensionEngine Input window located at DimensionEngine.com .

This tool was created so that engineering and physics problems would not have to be "solved by hand", as still frequently occurs in school and in the professional workplace. DimensionEngine does this work for you, so that the only way for an error to occur is to enter the wrong initial values or use the wrong equation. Everything else - all unit conversion, verification of dimensional consistency, and, of course, the actual computations - would be handled correctly by the computer. We wanted to make it as easy as possible to use and as hard as possible to make a mistake.

DimensionEngine:

Unlike many on-line tools for converting units, DimensionEngine is entirely text-based. You type the units you want exactly as you would write them down; there are no pull down menus to select types of units or units themselves. You can do calculations in the most convenient units - normally the ones you are initially given -- rather than having to convert them to an arbitrary standard system. You cannot make mistakes converting units because you never convert any units -- the computer does the conversion. Furthermore, because the input is text-based, you can easily copy, paste, and exchange your work. You do not have to input your work into a special window that "formats" your input. You do not have to learn special key strokes and exceptions.

DimensionEngine gives detailed error messages when your input is incorrect or inconsistent. If you request the output in units that are not compatible with the value calculated, DimensionEngine lets you know. It is difficult to make a mistake in your work and not realize it.

DimensionEngine allows you to define variables, and then use them in functions. You can solve nonlinear equations or optimize an objective function. A large library of standard math functions is included. This simplifies the process of engineering design, where the same set of calculations must be done iteratively to determine acceptable values. Unlike programs like Excel, the equations are clearly visible in the input and output, so you can easily check your work, spot mistakes and correct them.

This User's Guide gives a complete description of the syntax and functionality of DimensionEngine. It includes a large number of examples, so that people who learn best by doing can get up to speed as quickly as possible.

Top

2. Basic Syntax

Top

2.1 Converting Units

The fundamental components of the DimensionEngine calculator are the input window under the Input Tab that can be filled with lines of ASCII text, a "Calculate" button that submits the text in the input window to the DimensionEngine, and an output window of text under the Output tab which displays the results of all the conversions and calculations in the units requested by the user.

Except for user defined functions and commands to set options (see below), each line in the input file returns a value, which may be dimensionless or dimensional. To convert the output value into other units, simply list the units desired at the end of the line separated from the input value by a semicolon. The line can end in any number of different requested output units, each separated by semicolons.

For example, suppose we want to convert one inch into meters. The input and output after hitting the "Calculate" button would be the following

Input:
1 inch; meter





Simple unit conversion.

DimensionEngine numbers the input lines and repeats the input after the number. The next line then lists the output requested.

You can also simply type Shift-Enter instead of hitting the "Calculate" button.

To simultaneously see what one inch is in meters, millimeters, feet, yards, and miles, simply append all these units one after the other, each separated by semicolons. DimensionEngine recognizes the standard abbreviations for most units.

Input:
1 in; m; mm; km; ft; yard; mile





Multiple conversions of the same input

If you do not have a preference for the output, you don't have to request any. When no output units are requested, the output is given in the default unit system, which starts as meter-kilogram-second (MKS).

Input:
1 in





When no output units are given, the default is MKS units.

If you request an output unit that is incompatible with the dimensional value, an error message is printed and the value is given in the default units.

Input:
1 in; kg





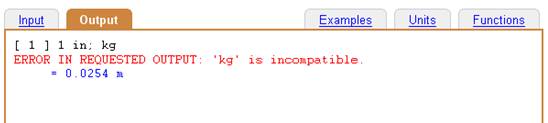
When the requested units are incompatible, an error message is given and the output value is displayed using the default units

Similarly, if you request an output unit that is not recognized by DimensionEngine, an error message is printed out and the value is given in the default units.

Input:
1 in; widgets





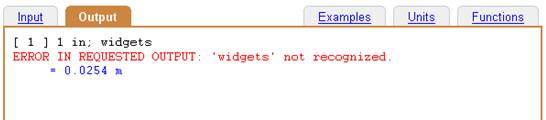
When the requested output units are not recognized, an error message is given and the output value is displayed using the default units

Because the Input and Output windows are saved separately, it is easy to go back to the Input text and correct any errors that are indicated or alter the problem.

DimensionEngine recognizes four standard default unit systems:

(The pound in IPS and FPS is lbf, not lbm). To use any of these systems, simply input in the system name. For example, to display the results using foot-pound-seconds, we type

Input:
FPS
1 cm
1 kg
1 N





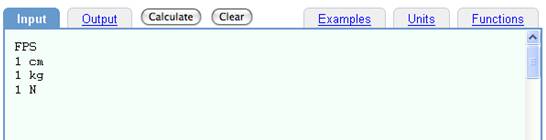
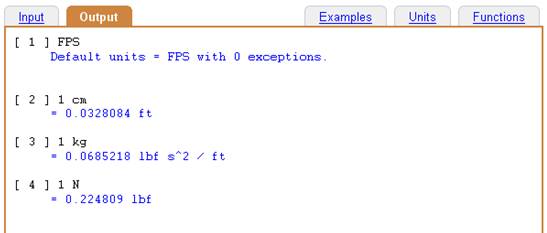
Output using the FPS (foot-pound-second) default system.

In this example, each of the four input lines has a separate, numbered output line. In line 3, one kg is converted to lbf s^2 / ft, which is the default units for mass in the FPS system.

In the above example, the output associated with the first input line, "FPS", is "Default units - FPS with 0 exceptions." Often, users want to define certain default output units to override the defaults. For example, the standard measurement of angle in all systems is radians, but often the user wants the output in degrees. Or, when analyzing mechanical moments, it can be preferable to display the output in "N m" rather than : "kg m^2 / s^2". When analyzing energy, it may be preferable to display the output in "J" rather than either "kg m^2 / s^2" or "N m", which are equivalent. To set exceptions to the default output units, simply list then in between the parentheses following the default unit system, separated by commas.

Some of the common default exceptions are:

Input:
MKS(deg, N)
q = 45 deg
f = 1 N
fx = f * cos(q)





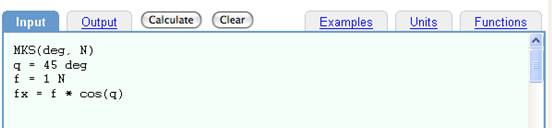
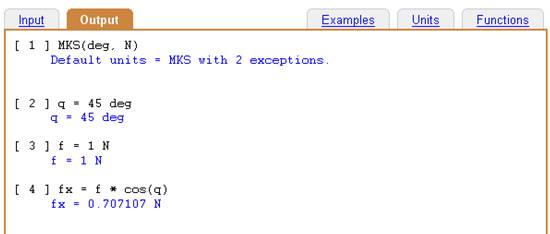
Requesting default output units.

Compare the above with what happens when the default is not requested:

Input:
q = 45 deg
f = 1 N
fx = f * cos(q)





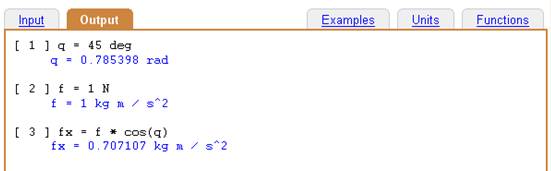
The same calculation without default output units.

When exceptions to the default output units are set (or reset), DimensionEngine goes through the list of exceptions, in order, to see if they are equivalent to the dimensions of the line's output value. If it is, then, that set of units is used to display the output. If no matches are found in the list of exceptions, the default units are used. (Since the exceptions are tested in order and stops as soon as a match is found, the statement "MKS(cm, mm)" is equivalent to "MKS(cm)".)

You can also use the MKS, cgs, IPS, and FPS as output units to force DimensionEngine to output a value in terms of the base units for each of these systems. This allows you obtain the output both in the units you want and broken down into base units on a single line of input. For example,

Input:
1 N; N; MKS; cgs; IPS; FPS





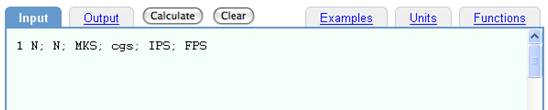
Explicitly requesting default output units.

Since DimensionEngine parses the text of any units, it has no trouble interpreting mixed and non-standard combinations of units, either in the input or in the requested output. For example,

Input:
2 slug m / hr^2; N; lbf; g in / min^2





Input and output using mixed and non-standard unit combinations.

You can always enter any values in the units in which you originally have them. There is no need to convert units. In fact, it is advisable NOT to convert any units, since that increases the chances of an error occurring.

DimensionEngine uses line-based, text input. The comment character is "#". This can occur anywhere in a line, and the rest of the line is treated as a comment that is displayed in the Output Window as part of the input line, but does not affect any computation. The line continuation character is "\". Blank lines can occur anywhere in the input text, and are often used to make the input easier to read. For example,

Input:
# The comment character is #
# Here is a an example of mixed units
2 slug m / hr^2; N # the answer should be 2.25215e-006 N

# The line continuation character is \
# Here is a single input line typed on two input lines
9.8 m \
s^2





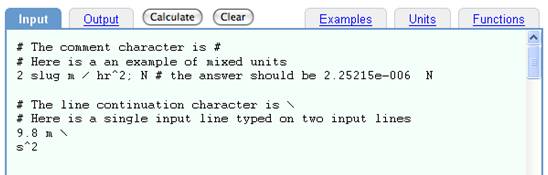
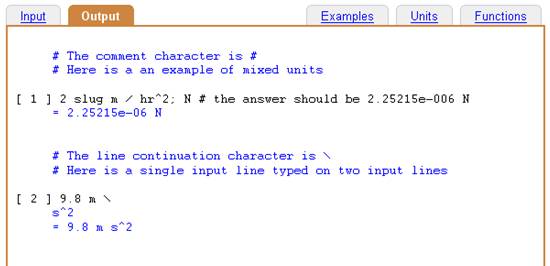
Using comments (#), line continuation (\), and blank lines.

Top

2.2 Variables and Dimensional Mathematical Syntax

Evaluating Mathematical Expressions

DimensionEngine is more than just a tool for converting units. DimensionEngine is a calculator that automatically and consistently converts units within mathematical expressions to produce the correct output and give the user appropriate error messages when mistakes and inconsistencies are found. In other words, DimensionEngine performs dimensional, symbolic mathematics.

The simplest example of this capability is adding, subtracting, multiplying, and dividing dimensional values. Simply types these in and DimensionEngine will correctly compute the results and display it in either the requested or default output units.

Input:
3 cm * 5 in + 10 ft^2





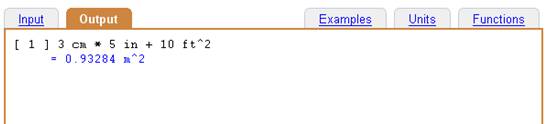
A simple, dimensional calculation.

It is often easier to define a variable for a dimensional value rather than type out its dimensional value every time it is used. This is especially true when the calculation is long, or when the same dimensional value is used many times. DimensionEngine uses the "=" to define variable names for dimensional values which can then be used in dimensional calculations. For example, the above example can be re-written as:

Input:
x = 3 cm
y = 5 in
z = 10 ft^2
x * y + z





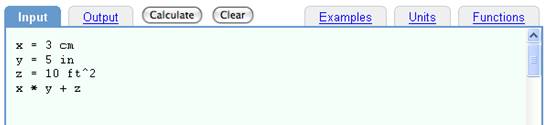
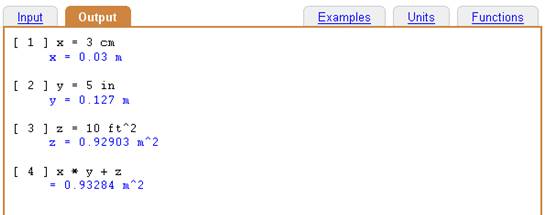
The simple, dimensional calculation of the previous example done using variables.

Order of Operations

As with any programming language, DimensionEngine defines an order in which operations are performed in order to unambiguously define how to interpret mathematical expressions. In many programming languages, the order of operations or order of precedence is:

Functions include mathematical functions such as exp( ) and sin( ). The use of this order or operations is illustrated in the expression

(4 + 10 / 2) / 9 = (4 + (10 / 2)) / 9 = (4 + 5) / 9 = 1

The order given matches programming languages such as Microsoft Office Excel in that negation has a higher priority than exponentiation, so

-3^2 = (-3)^2 = 9.

DimensionEngine adds a new operation to this list that assigns units to a dimensionless number. The full order of precedence in DimensionEngine is

Note that units can only be assigned to dimensionless numbers. Therefore, the expression

4 m

is correct because the units "m" is assigned to the dimensionless number 4. However, the expression

(2 in + 4 in) m = (6 in) m is an error in DimensionEngine

is incorrect because evaluation of the parentheses produces a dimensional value of 6 inches, which cannot be assigned to the unit "m". In other words, DimensionEngine does NOT interpret the expression as

(2 in + 4 in) m = (6 in) m = 6 in m = = 0.1524 m^2

Syntax Rules for Units

To make the syntax for DimensionEngine using the order of precedence unambiguous, we define explicitly what syntax is allowed when expressing the units that can be assigned to a dimensionless value.

Units syntax is simpler than mathematical syntax because there are fewer permissible operations. All unit expressions consist of a numerator and a denominator. The numerator and the denominator are composed of individual base units that can be raised to a power. In a units expression none of the following are allowed: variable names, functions, negation (except in the exponent), addition, or subtraction.

There are, of course, many different ways to define syntax for units expressions. DimensionEngine uses a syntax that: (a), most closely matches the syntax used when people use and write units; and, (b), has the least amount of typing. Sometimes, textbooks use special separators such as a dash or a dot between units that are multiplied together ( m - s or m &bull s). These separators are not allowed in DimensionEngine.

The following rules are used to interpret unit expressions in DimensionEngine:

Of these rules, the two that were most often considered for alteration were inserting an implied value of 1.0 (i.e., m = 1 m) in front of any unit expression if necessary and allowing 1 to be a base unit (i.e., 5 (1 / s)). This is straightforward to program, but was rejected for two primary reasons. First, this led to some odd, valid expressions such as "3 1 / 1 1 m / 3". Second, and more importantly, in our testing, in most cases, a missing or extra 1 was actually a typing mistake that we wanted DimensionEngine to catch and inform us about.

Other Syntax Rules

That completes the definition of DimensionEngine's syntax for mathematical expressions and unit expressions and unambiguously defines how DimensionEngine will interpret any input. However, there are still several important syntax rules that DimensionEngine uses.

Since DimensionEngine must be able to distinguish variable names, mathematical functions names, and dimensional base units, DimensionEngine uses the following rules for interpreting text names:

The most annoying of these rules is that variable names cannot match base units. Hence, "m", which would be a good variable name for a mass, is not allowed, since it the base unit for meter. We have attempted to strike a balance between recognizing as many common base units as possible while also permitting as many simple variable names as possible.

A full, alphabetical list of dimensional units recognized by DimensionEngine is located here.

A list of units by category is located here.

A list of units with one or two letters is located here.

We have not include "d" = day and "h" = hour in order to permit these letters to be used as variable names. We have included "mi" = mile, but excluded "Mx" = Maxwell (a good variable name for a moment in the X direction). Because variable names are case sensitive, M, f, a are valid variable names. In almost all cases, valid variable names can be composed using a letter followed by a number. So, m0, m1, and m2 are valid names for different masses.

Top

2.3 Mathematical Functions

DimensionEngine recognizes a large number of functions. These fall into the following categories:

A full alphabetical list of functions is located here.

A list of all the functions broken down by category is located here.

All of these functions are case insensitive. Nevertheless, some of the function names are written with capitals when this appeared to make the function easier to remember or use.

Below, we show a simple example using functions computing the weight of a baseball.

Input:
d = 9.39 in
r = d / 2
v = (4/3) * pi() * r^3
rho = 84 kg / m^3
w = grav() * rho * v; oz





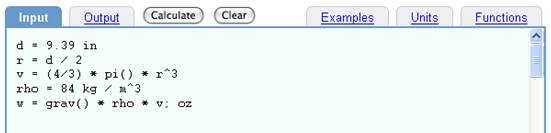
Using some functions.

For many functions, the argument (x) must be dimensionless. Some exceptions are the inverse trigonometric functions (which require angles, but see the Special Cases section); atan2, which requires two arguments with the same dimensions, LinInterp, where x1, x2, and x must have the same dimensions, and y1 and y2 must have the same dimensions; Number(x, units), which is used to retrieve a dimensionless number for the value of x written in the units expression "units".

Top

2.4 Three Dimensional Vectors

So far, we have only discussed scalar dimensional values. DimensionEngine also recognizes three dimensional vectors of dimensional values. These are defined by listing up to three, comma separated components between square brackets. All components of the vector must have the same dimensions, although these can be expressed using any compatible units expression. Note that a vector with dimensionless components is dimensionless, so the entire vector can be assigned units just as with a scalar value. Vectors cannot have more than three components. For example:

Input:
a = [ 1 in]
b = [2 ft, (3 + 4) in]; m
c = [5, 6, 7] m/s
d = [5 m, 4 kg, 0]
e = [1, 2, 3, 4]





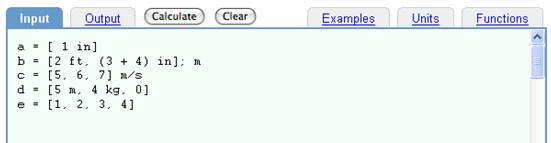
Vectors are assigned using square brackets.

The list of vector functions can be found here.

In addition, instead of using the component( ) function, one of the components of a vector with a variable name can be accessed simply by following the variable name with square brackets enclosing the component to access. For example,

Input:
x = [ 3, 4, 0]
q = atan2(x[2], x[1]); deg





Accessing components using the variable name.

The function PolarAngle does this same calculation.

Top

2.5 User Defined Functions

Many engineering calculations involve solving linear or nonlinear equations, or determining one or more dimensional values that optimize an objective function. DimensionEngine can do both of these.

DimensionEngine defines a syntax for specifying the function. A number of programs define functions explicitly in terms of variables. For example, in Microsoft's PowerToy calculator, you can define a dimensionless function by typing "f(x) = x * x". This creates a function called "f" that uses the variable "x" inside the function. When you call the function, "f(5)", it will replace "x" with the value "5" and then evaluate the function. Various other programs including Mathematica use similar syntax.

This syntax works for simple, one line mathematical functions but is a poor syntax for dimensional calculations. In many if not most real world calculations, the function computes more than one value that must be displayed. For example, when solving two linear equations for two unknowns, the solution must display both unknowns in whatever output units the user requests. In even moderately complicated problems, there are also auxiliary values that are computed whose value the user would like to know in the requested output units. It is difficult to construct a syntax for a single line that easily allows the different outputs to be displayed to be specified.

Instead, DimensionEngine takes advantage of the fact that its input consists of lines of input text. In DimensionEngine, only one function can be defined at a time, and the function is defined by whatever input text lies between the commands "BEGIN" and "END", which are not case sensitive and which must occur on their own lines.

For example, to duplicate the function "f(x) = x * x" defined above:

Input:
BEGIN
x = 4
f = x * x
END





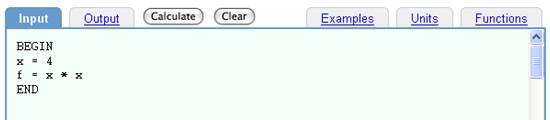
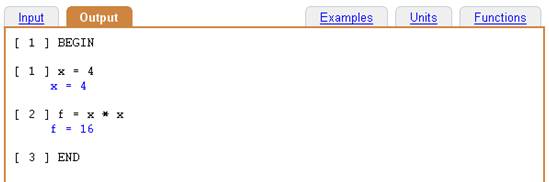
Defining the function f(x) = x * x

Notice that an initial value for x must be given, in this case, x = 4. This is similar to programming in Excel where cells must be given initial values. This format allows us to define what units, if any, the input values have, how they should be displayed in output, and verify the dimensional consistency of any equations. Of course, in simple, purely mathematical function, everything is dimensionless.

To evaluate f(5), we call the function "func(x, 5)" after the function is defined (i.e., after the END line).

Input:
BEGIN
x = 4
f = x * x
END
func(x, 5)





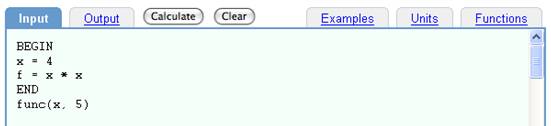
Evaluating f(5)

Once the call to "func" has been read, DimensionEngine goes back through and re-evaluates all the input lines between the most recent BEGIN and END. When it encounters any line that defines the value of x, it ignores the input text, prints the words "UPDATED VALUE", and then gives the specified value of the variable name. Notice that the function value "f" is simply printed out as part of the output. It does not have to be explicitly part of the func(x, 5) call - all lines in the function are re-evaluated and displayed in whatever requested output units needed. The re-evaluated lines are numbered "Func1", "Func2", etc. to distinguish them from the input text. If there is input text after the function call, that is evaluated after the function evaluation.

This syntax has several advantages. The lines of code can include and display all the auxiliary calculations associated with the function. In this respect, this is similar to MathCad's "workbook" concept, in which a series of linked calculations can be updated when an input value is changed and all of the outputs can be displayed.

func( ) is one of the functions that manipulate user supplied functions. The full list of functions can be found here.

All the arguments for fmax( ), fmin( ), and solve( ) must be variable names. They cannot be explicit calculations. In other words, with the simple function above f(x) = x *x, you cannot enter solve(x^2, x). Also, all function of function arguments must be scalars.

For example, suppose we want to find the minimum of cos(x):

Input:
MKS(deg)
BEGIN
x = 5 deg
y = cos(x)
END
fmin(y, x)





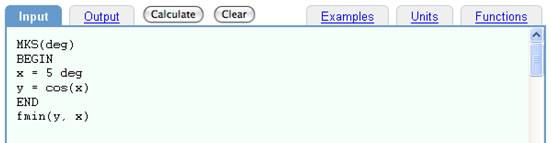
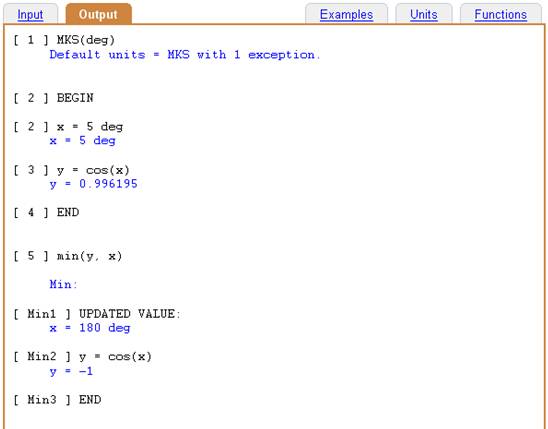
Finding the minimum of cos(x).

The underlying algorithms for solving equations and optimizing objective functions use general, nonlinear algorithms. For example, DimensionEngine does not attempt to determine if any solution involves linear equations and then explicitly find the exact solution using linear algebra.

Below, we show are lengthy example in which the static equilibrium solution for a physical system is found by summing the forces and moments and solving to make them all vanish. Notice that in the solution (lines numbered "Sol1" to "Sol11", the auxiliary quantities of each force and moment are updated and displayed in the FPS units requested.

Input:
FPS
r1 = [-5, -1] in
f1 = [10, -90] lbf
r2 = [2, 3] in
r3 = [0, 0] in
BEGIN
fx = 10 lbf # initial guess
fy = 10 lbf # initial guess
f2 = [fx, fy]
f3[1] = 10 lbf # initial guess
sumf = f1 + f2 + f3
summ = cross(r1, f1) + cross(r2, f2) + cross(r3, f3)
END
solve(sumf[1], sumf[2], summ[3], fx, fy, f3[1])







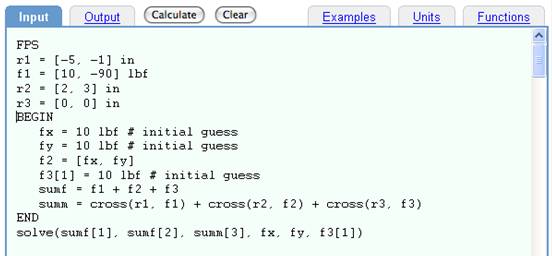
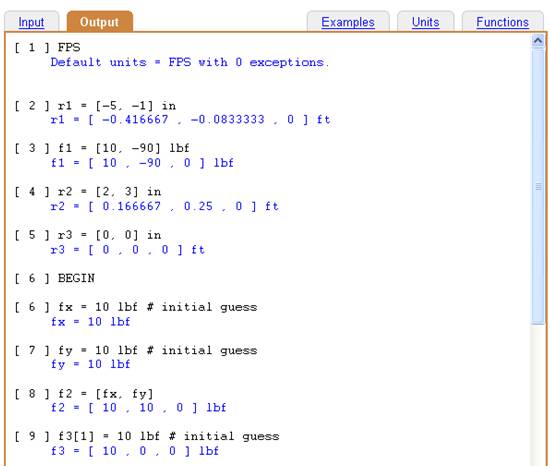
Solving a statics problem using the solve( ) function.

We can verify the accuracy of this solution by looking at lines Sol5 and Sol6 in which the sum of the forces and moments are computed.

One can debug the function by simply making leaving off the last input line ("solve(sumf[1], sumf[2], summ[3], fx, fy, f3[1])") and checking the output for errors. Once the function is correct, simply add the last line and re-submit.

Top

3. Special Cases and Exceptions

The syntax rules discussed in the previous section fully determine how DimensionEngine interprets dimensional input and performs dimensional calculations. Nevertheless, in many real world situations, things are actually done differently in practice. Or, as in the case of temperature, the one non-affine unit conversion recognized by DimensionEngine, they may not be fully defined by the rules of the previous section.

In this section, we review all the special cases that we have encountered and describe how they are handled in DimensionEngine. In some cases, these are simply clarifications of the syntax rules of the previous section; in other cases, they require additional rules or exceptions in order to produce the desires results.

Top

3.1 Base Unit lb

DimensionEngine assume that "lb" is "lbf". This is by far the most common use of "lb", although occasionally users mean "lbm", which can be confusing.

Top

3.2 Temperature

Temperature is always a special case for units conversion for two reasons:

  1. Zero degrees is not the same for all temperature units.
  2. Temperature is used in two distinct ways: sometimes it refers to an absolute temperature ("It is 10 degrees Fahrenheit today") while other times it refers to a temperature difference, i.e., a relative temperature ("It is 10 degrees Fahrenheit hotter than yesterday"). NOTE: When we use the term absolute, we are not referring to whether the scale is relative to absolute zero, only that it is not a temperature difference.

The formula for changing degrees Fahrenheit to degrees Celsius is:

degC = (5/9)(degF - 32)

To change the statement "It is 10 degrees Fahrenheit today" into Celsius, the full formula is needed:

(5/9)(10 degF - 32) = -12.22 degC

However, to change the statement "It is 10 degrees Fahrenheit hotter than yesterday", only the (5/9) part of the formula is used:

(5/9) (10 degFdiff) = 5.556 degCdiff

DimensionEngine has been designed a special syntax to distinguish these two cases so that it does the conversion intended by the user while keeping the syntax as close to common, real world use.

Specifically, DimensionEngine distinguishes the case where temperature is a single temperature base unit in the numerator (in which case it assumes an absolute conversion) from all other cases which are assumed to be relative conversion.

For example, in the example below we change absolute temperature. Because the units are all single temperature base units in the numerator, all of these are converted as absolute temperature.

Input:
1 degC; degF; degK; degR





A single temperature base unit in the numerator indicates absolute temperature conversion.

A single temperature base unit in the numerator indicates absolute temperature conversion.

If the single temperature base unit is moved to the denominator, the relative temperature conversion is performed:

Input:
1 / degC; / degF; degK^(-1); degR^-1





When a single temperature base unit is NOT in the numerator, relative temperature conversion is performed.

Whenever temperature units are embedded in other units (such as, for example, "J / degC") it is always interpreted as a relative temperature.

Sometimes, a temperature difference (i.e., relative temperature) is needed as an input quantity, such as in the example "It is 10 degrees Fahrenheit hotter than yesterday".

This is not directly possible with the "degF" base units. Instead, DimensionEngine defines four relative temperature based units degCdiff, degKdiff, degFdiff, and degRdiff, as illustrated below.

Input:
1 degCdiff; degFdiff; degKdiff; degRdiff





To input a relative temperature difference using a single base unit in the numerator, use degCdiff, degKdiff, degFdiff, and degRdiff.

To input a relative temperature difference using a single base unit in the numerator, use degCdiff, degKdiff, degFdiff, and degRdiff.

A real world example using relative temperature is thermal conductivity, where the rate of heat energy conducted through a flat object is proportional to the temperature difference on either side of the object. The example below computes how much thermal energy flows through three inches of insulation.

Input:
delT = 21 degCdiff
k = 0.20 J / s m degC
w = 3 in
a = 10 m^2
h = k * a * delT / w; J/s





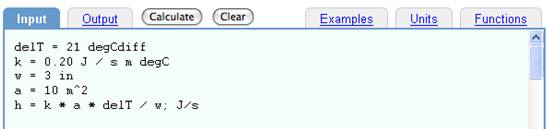
Thermal conductivity: a real world example using relative temperature units.

Of course, one could also obtain relative temperature differences by entering input two different absolute temperatures and then subtracting them, but this can be cumbersome. In the example above, we could define T1 = 25 degC, T2 = 4 degC and then replace delT in the final formula by (T1 - T2).

Occasionally a formula uses combinations of absolute temperature. For example, in radiant heat, the formula involves absolute temperature to the fourth power. Because of the exponentiation, DimensionEngine will interpret degC^4 as a relative temperature. DimensionEngine does not provide a method for combined, absolute temperature conversion. Instead, the absolute temperature should be input in degC as a distinct input, and then the combination (raising to the fourth power in this case) should be done as a separate formula calculation. The example below computes the net heat flow due to radiation from a person standing in room temperature air:

Input:
T_person = 98.6 degF
T_air = 72 degF
a = 1.5m^2 # surface area
e = 0.70 # emissivity
h = e * StefanBoltzmann() * a * (T_person^4 - T_air^4); W





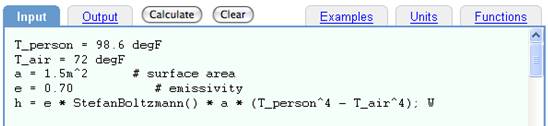
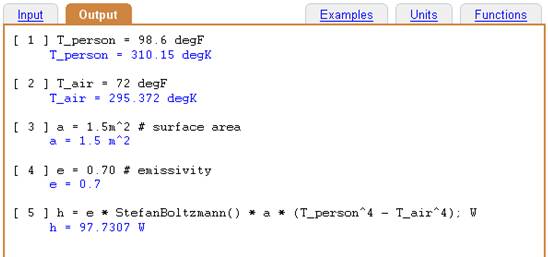
To use absolute temperatures in a formula such as thermal radiation, enter any temperatures as separate variables.

Top

3.3 Radians and Other Angular Measurement Units

Because DimensionEngine was designed to do as much of the unit conversion as possible in dimensional calculations, radians and other angular measurements cannot simply be treated as a dimensionless number.

Formally, a radian is dimensionless, and the simplest and most common method of handling radians, degrees, and revolutions is to treat them as dimensionless values. For example, on many hand calculators, when you enter

sin(45)

the calculator defaults to interpret this as sin(45 radians), unless the user selects an option to have all arguments to trigonometric functions default to degrees. However, practical problems arise with this approach as soon as other units are considered because in the real world angular measurement is often not simply interpreted as a dimensionless number.

First, if radians are truly dimensionless, then it is impossible to distinguish circular frequency (radians per second) from linear frequency (inverse seconds) because these two units are identical. When using circular frequency in calculations, rather than having DimensionEngine take care of the units for the user, the user would be responsible for explicitly inserting appropriate values of 2? whenever necessary. This is undesirable.

Second, if one of the default output units is degrees, then, all dimensionless numbers would be converted to degrees, including ones that have no angular interpretation. This would be very confusing. In fact, if this approach were taken, then we would have to create a new base unit for true dimensionless numbers so that users could explicitly override a default such as degrees.

For these reasons, DimensionEngine treats angular measurement as a distinct unit even though this is "formally" incorrect. This corrects the above two problems.

Of course, this also means that DimensionEngine thinks sin(45) and sin(45 rad) have different arguments. However, by default, DimensionEngine can accept either a dimensionless number or an angular argument for all trigonometric functions, so both sin(45) and sin(45 rad) give the same answer.

Top

3.3.1 Exception #1: Adding and Subtracting Radians and Dimensionless Numbers

The approach just described works well in practice, but some exceptions arise. Occasionally, formulas are used which explicitly utilize the fact that radians are formally dimensionless numbers. For example, occasionally one runs across formulas such as

x = 2 rad
y = x + sin(x)

If DimensionEngine followed the formal syntax, then it would not allow the addition of an angular value (x) and a dimensionless number (sin(x)). However, since this is not the expected result for most users, DimensionEngine allows this, and returns a value that is dimensionless.

Notice in the example below that y0 and y1 are returned as dimensionless numbers, not numbers with angular units (e.g., rad).

Input:
x0 = 3
y0 = x0 + sin(x0)
x1 = 1 rad
y1 = x1 + sin(x1)





Combining angular units and dimensionless numbers.

Top

3.3.2 Exception #2: Multiplying Angular Measurements (Radians) by Length

One of the well known and frequently used calculations is to multiply circular frequency by a radius to obtain linear velocity. This is just one of a class of problems in which a dimensional value with units incorporating radians is multiplied by a dimensional value that incorporates length units. In these cases, it is customary to strip the radians from the result (i.e., treat radians as a truly dimensionless unit). Because this operation occurs so frequently, this has been programmed into DimensionEngine.

Input:
om = 50000 rpm
r = 6 cm
v = om * r
a = v^2 / r





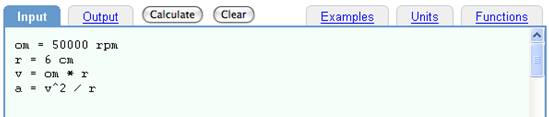
Multiplication of angular measurements by length

In the example above, the resulting values for v and a do not include radians.

Top

3.3.3 Base Units for Circular and Linear Frequency

As discussed previously, DimensionEngine explicitly distinguishes circular frequency (radians per second) and linear frequency (inverse seconds). Because of this, there are several base units which also incorporate this distinction.

The two base units for circular frequency (radians per second) are:

The base units for linear frequency (inverse seconds) are

User should be careful not to confuse rps and Hz, as they are not the same in DimensionEngine.

Top

3.4 Is Zero Dimensionless?

The number zero is special: one can easily argue that the number zero has all dimensions, or no dimensions, or something between. However, in an application such as DimensionEngine, it definitely has a unique set of dimensions associated with it, just like all values in DimensionEngine.

However, when inputting vectors, all of whose components must have compatible units, it is often convenient to assume that any zeros have whatever the appropriate units are to make the vector correct. This only applies to zero as an argument in a vector.

Input:
f1[2] = 2 lbf
f2 = [0, 2 lbf, 0]
f3 = [1, 2 lbf, 0]





Using zeros when inputting vectors.

Top

3.5 Tolerance for Non-Integer Exponents

DimensionEngine uses a tolerance value of 10e-5 when comparing exponents on units so that m^(1/3) is the same as m^(0.33333) but not m^(1/3) is not equal to m^(0.3).

Input:
5 m^(1/3); m^(0.33333); m^(0.3)





Tolerance for non-integer exponents.

Top

3.6 The Number Function

The Number function creates a dimensionless value from a dimensional value. For example, to extract the dimensionless value of a length measurement in cm,

Input:
x = 2 ft
y = Number(x, cm)





The Number function.

Top

4. Legal

The software described in this document contains valuable trade secrets and proprietary information and is protected by the copyright laws of the United States. It may not be copied or distributed in any form or medium, disclosed to third parties, or used in any manner without written prior approval. Unauthorized use of software or its documentation can result in civil damages and criminal prosecution.

DimensionEngine is to be used at the users own risk. We make no representations or warranties, express or implied, about the accuracy of this software. By way of example, but not limitation, we make no representations or warranties of the merchantability or fitness of DimensionEngine for any particular purpose or that the use of this software, components, or documentation will not infringe any patents, copyrights, trademarks, or other rights. Certain features of DimensionEngine are patent pending.

Top