Manning’s equation relates the discharge of a stream to its geometry and roughness as
where R is the hydraulic radius (cross sectional area divided wetted perimeter) and km is a units constant equal to 1.0 m1/3/s = 1.49 ft1/3/s (i.e, if R is in units of meters, km = 1.0 m1/3/s and v will be have units of m/s).
Manning's n is often estimated for a given reach using tables such as Table 9.6 in Dingman (Physical Hydrology, Prentice Hall, 2002). For example for small streams with rocky beds and moderate slopes, Manning's n is usually in the range 0.03 - 0.05. Alternatively, it is possible to directly determine Manning's roughness coefficient. This is done using a topographic cross section of the stream, a measurement of the downstream water surface slope, and a direct measurement of discharge.
As an example, consider the topographic cross section shown below. Note that the data indicate the current stage of the stream (8.23 m above some arbitrary but fixed datum).
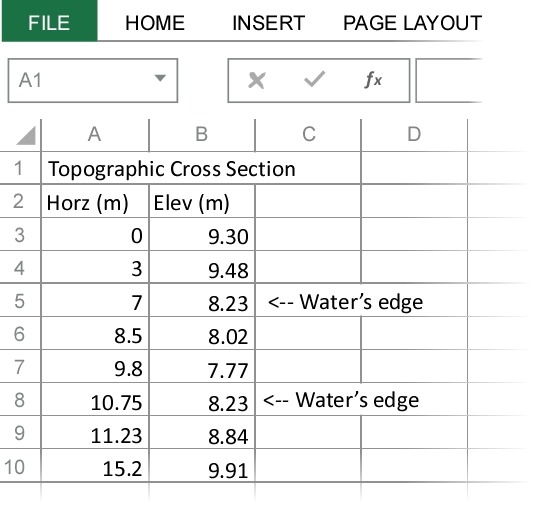
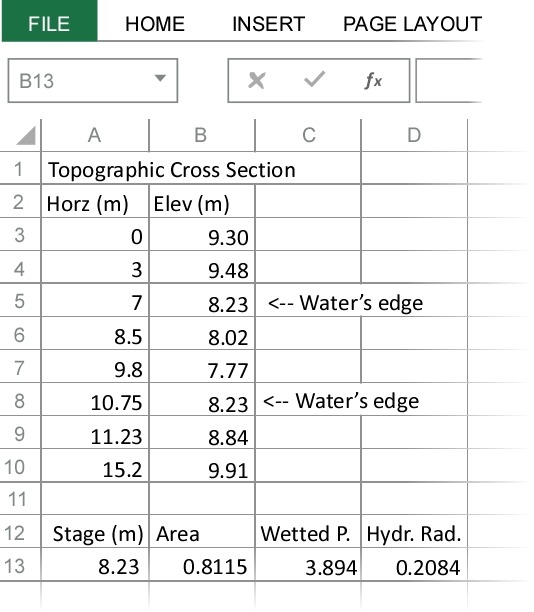
1) Create a new entry labeled “Stage (m)” and enter 8.23 - the water level. Next to this cell, create a another new entry labeled “Area (m^2)”. Now place the cursor in the cell under the Area label and next to the cell containing 8.23, then select the command to insert a function. Select the HydroTools category and then the ChannelArea() function. Enter the cells containing the distances, elevations, and stage, as directed. Then press return. The function automatically returns the cross sectional area of the channel at that stage.

2) Next to the Area column, create a new column called “Wetted Perimeter (m)”. Use the HydroTools function WettedPerimeter() to calculate the wetted perimeter of the channel at this stage.
3) Using the Area and Wetted Perimeter, calculate the hydraulic radius (channel area divided by wetted perimeter) at this stage.
4) Calculate the average stream velocity by dividing the measured discharge Q by the channel area A.
5) With the measured water slope you now have all the numbers you need to back-calculate Manning’s n for this cross-section using Manning's equation give above.